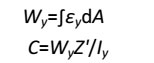摘要:本文结合固有应变理论、有限元数值模拟技术及激光焊接实验三种方法:利用固有应变法计算薄板对接焊变形量;运用Marc有限元分析软件对激光对焊接薄板模型进行数值模拟;对比300W激光焊接1mm奥氏体304 薄板不锈钢变形量。探讨薄板激光焊接预测的准确程度及夹具夹持位置对控制变形的有效程度。结果表明:有限元模拟结果与焊接试验对比,模拟变形量与实际相差10%;固有应变法计算薄板对接焊变形量与实际相差15%。此外,通过施加夹具前后变形量对比发现,夹具夹持后的变形量减少了77%,夹具夹持对控制薄板激光焊接变形效果显著。
0.引言
在激光焊接过程中,因为激光能够向工件传输很高的能量密度,形成深宽比较大的焊缝,而且焊接飞溅少、热影响区小、焊缝成形美观等优点,它在焊接领域已经得到了越来越广泛的应用[1]。近些年来,不锈钢薄板的应用范围更加广泛,在航空航天、电子器件、医疗器械、核工业、机械仪 表等方面的应用越来越多。因此,不锈钢薄板的焊接变得十分重要[2]。传统的焊接方法难以保证薄板的成型质量,而激光焊接具有传统焊接无法比拟的优点,能有效减少焊接缺陷[3]。然而,对于薄板焊接,激光焊无法避免焊接过程中产生的焊接变形,影响结构的制造精度和使用性能。因此,为了控制和减小焊接变形,有效预测激光焊接不锈钢薄板的变形工作很有实际意义[4]。
对于焊接变形的估计过去大多基于经验或简化计算方法,只能用于最简单的板或梁等焊接结构,对稍复杂的焊接结构就无能为力[5]。
固有应变法和有限元数值模拟是两种既能解决大型复杂结构,又比较经济的预测焊接变形的方法,有很大的实用意义和发展前途[6]。
本文结合固有应变理论、有限元数值模拟技术及激光焊接实验三种方法:利用固有应变法计算薄板对接焊变形量;运用Marc有限元分析软件对激光对焊接薄板模型进行数值模拟;对比300W激光焊接1mm奥氏体 304薄板不锈钢变形量。
1.试验材料和方法
采用半导体激光焊接设备10对两块尺寸为200×50×1mm的304不锈钢薄板进行对接焊,激光波长1.06μm,最大输出功率为500W。进行3组同参数试验减小试验误差。为了更直观地展示其变形程度,焊接过程不施加夹具,选用氩气作为保护气体。连续激光焊接的工艺参数参见表1,待焊薄板 尺寸如图1所示。

对焊接板的纵向最大弯曲挠度进行测量,如图2所示;利用固有应变法计算薄板激光焊接后的 纵向变形量;利用Marc数值模拟软件,通过网格划分,添加材料性能参数,施加边界条件,添加热 源模型等步骤,对实际焊接情况进行模拟;将理论计算变形值和模拟的薄板纵向变形值与实际变形量进行对比,验证固有应变法和数值模拟是否能有效预测薄板的焊接变形。

2.固有应变分析
对于简单的梁或者平板的焊接变形,可以用残余塑变进行简化计算[7]。焊接变形可以分为纵向变形和横向变形,这里我们假设其变形分别是由纵向和横向残余塑变引起的[8]。对于本实验来说重点是要计算z轴方向的残余塑变,因为x和y方向的变形量很小,而且其变形可以通过刚性约束以及底板装配二次焊接来校正,所以我们这里只计算z轴方向的最大弯曲挠度。
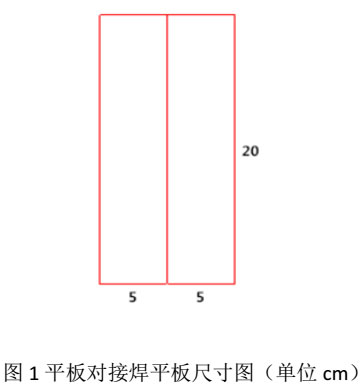
如果已知单位长度上纵向残余塑变εy的总和Wy,则有[9]:
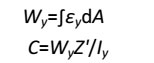
式中,C为曲率;Iy为截面惯性矩;Z'为Wy中心到截面中心距离。试验和理论的研究指出,对于单道焊当构件刚性较大时,存在纵向收缩单位体积Wy和焊接线能量qv的正比关系[10]:

式中qv为焊接线能量(J/cm2);η为电弧热效率;P为焊接功率(W);v 为焊接速度(cm/s);f 为最大弯曲挠度;L为板长(cm)。
计算得 Iy=1/1200,对于激光焊接 η=0.9,P=300 W,v=2 cm/s。代入得 f=2.72 mm。
3.有限元分析模型
3.1.模型的建立及网格划分
对薄板对接焊进行模拟,根据热源的输入范围给出了明晰的焊接接头有限元分析建模的规划方法及单元划分的思路,力求做到单元形状规则、疏密分布合理,我们提出了一条比较明晰的思路: 先建立XY平面,分为40*200个单元,在X方向上设置疏密过渡,偏置系数为0.3;利用网格拉伸的 方法,向Z向两次拉伸,每次拉伸0.5mm,完成三维的模型建立和网格划分。
先用分区域划分的方法,划分焊缝某一截面的网格,力求做到网格疏密分布合理,然后将面网格拉伸成体网格,利用Marc中的复制功能完成体网格的填充(如图3所示)。这样划分出的网格在减小计算量的情况下兼顾了计算的精度。

图3中对接焊有限元模型尺寸为50mm*200mm*1mm,由于对称性取其一半进行建模,为了保证计算精度缩短计算时间对过热区采用了过渡网格的方式。
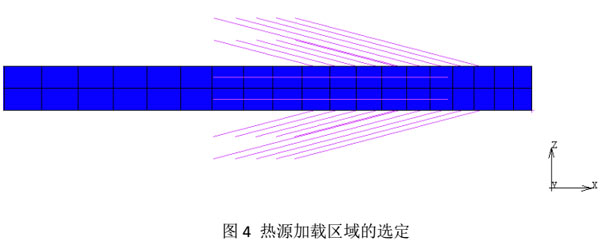
图4中选择细分网格的1mm区域作为热源加载区,根据是实际焊接热源的深度和宽度与之匹配。
3.2.材料性能参数及边界条件处理
由于材料的物理性能(如比热、屈服强度、热膨胀系数及导热系数等)都和温度等变量有关, 所以首先必须定义这些性能和温度等变量的关系。由于 304 不锈钢的物理性能参数在 Marc 的材料库 里存在,所以直接引用。
环境的初始温度设置在20℃。在定义边界条件时,由于在焊接过程中试件是固定的,根据实际 的情况固定X,Y,Z三个方向来达到焊件位移为0的目的。焊接过程中存在母材与外界环境的热交换(忽略夹具与母材的热交换),选择表面散热,对称面绝热,定义环境温度为20℃,散热系数为0.05。散热边界条件处理后如图5所示。

设定好焊缝单元以及焊接路径,并依据体热源模型参数的选取方法选取热源模型参数,收敛准则采用residuals and displacements,收敛容差均设定为0.01,采用瞬态求解方法,在求解其中选择大变形求解条件,输出结果设置为Stress和Equivalent VonMises Stress,最后提交求解直到求解完毕退出号为3004即得到正确结果。
4.结果分析及准确性验证
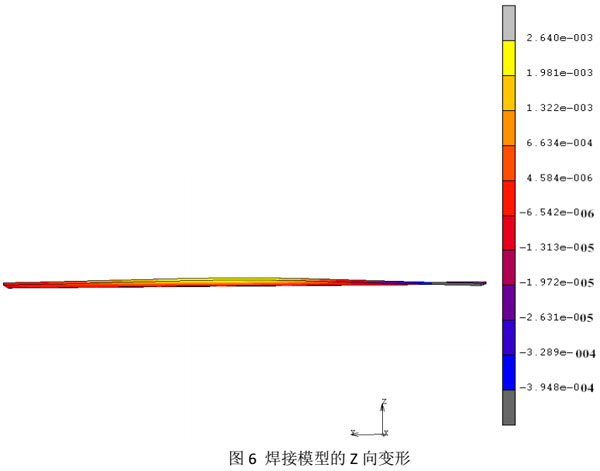
薄板对接焊后,发生了较明显的Z向变形和角变形。本文的一个重要目的是为了预测薄板对接的Z向变形量,模拟变形云图如图6,焊缝中心横向路径上Z向的变形值最大,约为2.6mm,从中心往两边变形量逐渐减小。模拟的变形结果和焊接试验结果很相似,都是薄板在纵向上出现较明显的弯曲变形;弯曲挠度最大值都出现在垂直于焊缝中心的路径上;最大弯曲挠度值相差很小。
结合之前的焊接试验和理论计算,薄板的变形的试验结果、理论结算结果与数值模拟的结果数据均记录在表2

通过对以上固有应变理论计算、有限元计算结果与试验测得薄板的最大变形量分析对比可知,理论计算和数值模拟的焊接变形与试验结果很接近:模拟变形量与实际相差10%;固有应变法计算 薄板对接焊变形量与实际相差15%。由此可以说明焊接变形量的固有应变理论计算和有限元分析是可靠的,且有限元数值模拟更优于理论计算,这对预测焊接变形有着极其重要的意义。
5.夹具法控制变形
为了有效地控制变形,设计如图7、8所示夹具,得出焊接变形量。如图7、8所示,平台固定装置有6只完全相同的夹具,由于一般的平板长度都在200mm以内,通常只用平台后四个夹具进行夹持。两夹具之间纵向装配距离为120mm。


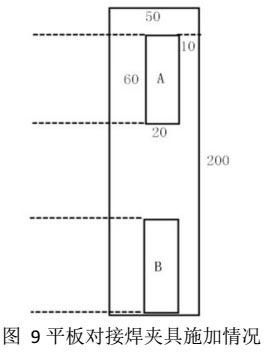
范围只有20mm*60mm,本次选用的夹具A和B施加在距对接焊接口10mm处,A夹具距板上边缘距离为20mm,如图9所示。对薄板焊后的弯曲挠度进行测量,记录在表3中

6.结论
(1)有限元模拟结果与焊接试验对比,模拟变形量与实际相差10%;
(2)固有应变法计算薄板对接焊变形量与实际相差15%。
(3)通过施加夹具前后变形量对比发现,夹具夹持后的变形量减少了77%,夹具夹持对控制薄板激光焊接变形效果显著。
参考文献:
[1]李亚江, 李嘉宁. 激光焊接/切割/熔覆技术[M]. 北京: 化学工业出版社, 2012.
[2]于启湛, 丁成钢, 史春元. 不锈钢的焊接[M]. 北京: 机械工业出版社, 2009.
[3]张维哲. 304 不锈钢薄板激光焊接技术研究[硕士学位论文]. 大连: 大连理工大学, 2009.
[4]汪建华, 陆皓. 预测焊接变形的残余塑性应变有限元方法[J]. 上海交通大学学报, 1997, 31 (4):53‐56.
[5]汪建华. 焊接数值模拟技术及其应用. 上海: 上海交通大学出版社, 2003. 10.
[6]王长生, 薛小怀, 楼松年. 薄板焊接变形的影响因素及控[J]. 焊接技术, 2005, 8: 66-68.
[7]Yu Fan. Mechanical Properties of leaser Beam Weld Ti6Al4V[D]. Nottingham: The University of Nottingham, 2010.
[8]Ueda Y, Kim YC, Yuan MG. A prediction method ofwelding residualstress using source of residual stress(Report I) Characteristics of in‐herent strain(source of residual stress)[J]. J Trans. Of JWRI, 1989, 18 (1): 135‐141.
[9]Masubuchi. Prediction and control of residual stresses and Deformation in welded Proc.Theoretical Prediction in Joining and Welding, 1996: 71‐88.
[10]谢元峰. 基于ANSYS 的焊接温度场和应力的数值模拟研究[D] .武汉: 武汉理工大学物流工程学院, 2006.